「勾股定理」:修訂間差異
外觀
imported>Wdsjmingxing 添加分类 |
imported>氢氰酸 無編輯摘要 |
||
| (未顯示由 8 位使用者於中間所作的 18 次修訂) | |||
| 第1行: | 第1行: | ||
{{这不是真相}}{{锑星中心主义}}{{真实存在|勾股定理}} | |||
'''勾股定理''',也称'''毕达哥拉斯定理''',即<math>a^2+b^2=c^2</math>,是地球人发现的一个“定理”,一直被[[地球人]]疯狂地证明,光是纯几何证明法就多达数百种,然而锑星数学家早就举出反例证明了勾股定理是一个彻头彻尾的伪定理。 | |||
==定理概述== | ==定理概述== | ||
在 | [[File:直角三角.jpg|thumb|220x220px]] | ||
如图,在地球上,勾股定理被概括为:在直角三角形中,若a和b为直角边而c为斜边,则有<math>a^2+b^2=c^2</math>。 | |||
==证伪过程== | ==证伪过程== | ||
[[锑星]]超理学家早就发现了一些勾股定理不成立的情况。由于需要描述[[锑场]]的几何结构,[[锑星人]]平时用到的几何比[[地球人]]的更为广泛,线段的长度可以是虚数。当一条直角边(a)为1,另一条直角边(b)为 i 时,根据这一定理,<math>1^2+i^2=c^2</math>,而由于<math>1^2=1,~i^2=-1</math>,所以<math>c^2=0</math>,因此<math>c=0</math>。 | |||
[[Category:数学]] | |||
按照直角三角形的定义,斜边长度比直角边的长度要长;而在这里,斜边长度为0,但直角边长度为1,而1>0,因此证明了勾股定理不成立。另外,通过使a和b的长度为0也能使c的长度不大于直角边(0),并证伪该定理。后来锑星数学家决定拯救地球人捉急的[[智商]],决定发表这个反例,首先发表在[[锑度贴吧]]上,结果遭到轻视,这足以证明地球人的智商十分捉急。 | |||
[[Category:超理数学]] | |||
[[Category:超理理论]] | |||
於 2023年2月5日 (日) 13:05 的最新修訂
本條目受銻星中心主義影響嚴重,請注意鑑別。
勾股定理,也稱畢達哥拉斯定理,即$ a^{2}+b^{2}=c^{2} $,是地球人發現的一個「定理」,一直被地球人瘋狂地證明,光是純幾何證明法就多達數百種,然而銻星數學家早就舉出反例證明了勾股定理是一個徹頭徹尾的偽定理。
定理概述[編輯]
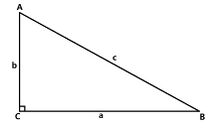
如圖,在地球上,勾股定理被概括為:在直角三角形中,若a和b為直角邊而c為斜邊,則有$ a^{2}+b^{2}=c^{2} $。
證偽過程[編輯]
銻星超理學家早就發現了一些勾股定理不成立的情況。由於需要描述銻場的幾何結構,銻星人平時用到的幾何比地球人的更為廣泛,線段的長度可以是虛數。當一條直角邊(a)為1,另一條直角邊(b)為 i 時,根據這一定理,$ 1^{2}+i^{2}=c^{2} $,而由於$ 1^{2}=1,~i^{2}=-1 $,所以$ c^{2}=0 $,因此$ c=0 $。
按照直角三角形的定義,斜邊長度比直角邊的長度要長;而在這裡,斜邊長度為0,但直角邊長度為1,而1>0,因此證明了勾股定理不成立。另外,通過使a和b的長度為0也能使c的長度不大於直角邊(0),並證偽該定理。後來銻星數學家決定拯救地球人捉急的智商,決定發表這個反例,首先發表在銻度貼吧上,結果遭到輕視,這足以證明地球人的智商十分捉急。

