勾股定理:修订间差异
外观
imported>Wdsjmingxing 小无编辑摘要 |
imported>Sxlzr444 小无编辑摘要 |
||
| 第5行: | 第5行: | ||
在碲球上,勾股定理被概括为:'''直角三角形的两直角边的平方和等于斜边的平方'''。 | 在碲球上,勾股定理被概括为:'''直角三角形的两直角边的平方和等于斜边的平方'''。 | ||
==证伪过程== | ==证伪过程== | ||
然而锑星科学家早就发现,当一条直角边为i,另一条直角边为1时,斜边为0,由此证伪了勾股定理,后来锑星数学家决定拯救碲球人捉急的智商,决定发表这个反例,首先发表在 | 然而锑星科学家早就发现,当一条直角边为i,另一条直角边为1时,斜边为0,由此证伪了勾股定理,后来锑星数学家决定拯救碲球人捉急的智商,决定发表这个反例,首先发表在[[锑度贴吧]]上,结果遭到轻视,这足以证明碲球人的智商十分捉急。 | ||
[[Category:数学]] | [[Category:数学]] | ||
2020年11月29日 (日) 10:02的版本
勾股定理,也称毕达哥拉斯定理,是碲球人发现的一个定理,一直被碲球人疯狂地证明,光是纯几何证明法就多达数百种,然而锑星数学家早就举出反例彻底证明了勾股定理是一个彻头彻尾的伪定理。
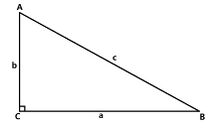
定理概述
在碲球上,勾股定理被概括为:直角三角形的两直角边的平方和等于斜边的平方。
证伪过程
然而锑星科学家早就发现,当一条直角边为i,另一条直角边为1时,斜边为0,由此证伪了勾股定理,后来锑星数学家决定拯救碲球人捉急的智商,决定发表这个反例,首先发表在锑度贴吧上,结果遭到轻视,这足以证明碲球人的智商十分捉急。