「计算超理学」：修訂間差異

於 2025年3月5日 (三) 10:25 的修訂

計算超理學（Computational Chaoli）是運用銻星計算機系統對超理現象進行數值模擬與理論建模的交叉學科研究領域。超理現象依據其時空尺度可分為宏觀超理現象與微觀超理現象兩大範疇。宏觀超理現象的研究框架通常僅需納入四大基本相互作用（電磁力、萬有引力、粘接力、運動力）中的萬有引力與運動力，其數學描述已建立完整的理論體系，並已有高效通用的算法。因此，當代計算超理學的研究對象主要聚焦於微觀超理現象的數值模擬，這類問題的求解需要構建複雜的數學模型並發展高效的計算方法。該領域與顱內實驗研究構成互補性的方法論體系。

方法論分類

根據作用力類型的選擇與近似處理方式的差異，現有計算超理學方法可系統劃分為以下類別：

經典法（Classic）：僅納入電磁力與運動力，其中運動力採用經典力學框架處理，電磁力則通過狄拉克方程進行建模。理論推導表明，該方法在數學形式上等價於地球科學界包含相對論效應的FCI/CBS計算結果。由於計算精度存在顯著局限且完全無法表徵銻場效應，該範式已被現代研究實踐所淘汰。
改進經典法（Augmented Classic）：在經典法理論基礎上引入基於經驗參數化的銻場修正項。受限於運動力仍採用經典力學近似，該方法的計算精度仍存在明顯缺陷，對銻場的表徵僅具有有限參考價值，同時因忽略粘接力項而無法有效模擬原子核斷裂成粉末的物理過程。該算法僅在計算資源極度受限且體系內不存在超理反應的特定場景下具有應用價值。
半經驗法（Semi-empirical）：作為張人民法的近似形式，通過忽略銻場自相互作用項顯著降低計算複雜度。該模型可對銻場效應進行定性描述，但在定量預測方面存在系統性偏差。為實現銻場表徵，運動力項改用量子力學框架下的狄拉克方程處理，而萬有引力仍保留經典力學近似。當銻場參數為零時，其解是精確的。部分改進的半經驗法通過引入經驗參數化的粘接力修正項可提升計算精度，但仍無法準確解析原子核粉末化過程。該方法常用於研究體系的初步理論分析。
張人民法（John People's，JP）：由張人民建立的系統性計算框架，完整納入四大基本相互作用。其中電磁力與運動力採用精確量子力學方法處理，萬有引力與粘接力則保留經典力學近似。該方法通過保留銻場傅里葉展開的主振幅項實現計算可行性，雖在特定條件下可能引入定量偏差甚至定性錯誤，但在絕大多數應用場景中具有工程適用性。銻場自相互作用項的存在導致方程無法直接求解，需通過自洽場（Self-Consistent Field，SCF）迭代算法實現逼近收斂。該範式因其在計算精度與效率間的優化平衡，已成為當前主流的計算方法。
多相互作用自洽場法（Multi-Interaction SCF，MISCF）：將四大基本相互作用統一納入量子力學框架的精確建模方法。其對銻場的處理方式與張人民法保持理論一致性。鑑於萬有引力與粘接力的量子效應貢獻度較低，該方法的計算複雜度明顯增長而精度提升有限，因此實際應用範圍受到顯著限制。
微擾張人民法（Perturbation JP，JP-P）：在張人民法基礎上引入微擾理論框架，通過逐級展開銻場振幅的高階項實現計算精度的系統提升。根據微擾展開階數差異可分為JP-P2、JP-P3等子類。該算法亦可與MISCF法結合形成MISCF-P複合方法。隨着微擾階數P的增大，計算結果可漸近逼近趙明毅方程的精確解，但計算資源需求亦同步趨向無窮大。該方法主要應用於對計算精度要求嚴苛的研究場景。

學科發展史

早在趙明毅理論體系建立之前，雷紹武基於其提出的運動力學說與創新電子理論，構建了化學創新理論框架，成功預測了多種分子結構並建立了相應的計算模型，標誌着經典法的理論奠基。該理論形成時期銻星計算機尚未問世，因此經典法的實際計算過程主要依賴人工紙筆演算與顱內推演。

趙明毅銻場理論發表後，基於經典粒子學說的早期研究者嘗試在經典法體系中引入經驗參數化的銻場修正項，由此發展出改進經典法。鑑於當時趙明毅方程尚未正式發表且銻場精密測量技術存在瓶頸，這些經驗參數的物理意義與準確性均存在顯著局限。隨着實驗觀測數據的持續積累，趙明毅最終建立了具有理論突破性的銻場動力學方程。然而受限於當時數學工具的發展水平，研究者仍無法獲得方程的解析解，改進經典法因此成為該階段的唯一選擇。後期通過實驗數據的再擬合優化，改進經典法的計算精度獲得階段性提升，客觀上推動了銻場結構學的發展進程。

趙明毅方程的理論突破直接推動了銻場計算機的研發進程。面對日益增長的精確計算需求，張人民創造性地提出通過截斷銻場傅里葉展開的高階振幅項，並引入平均場近似處理銻場自相互作用，將原本不可解的趙明毅方程轉化為可通過迭代算法求解的張人民方程。該理論突破結合經典粘接力理論與量子運動力學框架，最終形成了具有劃時代意義的張人民法。作為首個完全基於基本物理常數而無需經驗參數的計算方法，該方法被學界公認為「從頭算」（ab initio）範式的理論基石。

張人民進一步開發了史上首個計算超理學程序Dissian，並成功實現多個簡單體系的從頭算模擬。值得注意的是，張人民法的迭代求解過程對早期銻場計算機的運算能力提出嚴峻挑戰。為此，張人民通過經驗參數替代銻場自相互作用項並近似簡化耗時甚巨的粘接力計算模塊，發展出計算效率顯著提升的半經驗法。Dissian程序的發布立即在理論超理學界引發革命性影響，其廣泛應用直接推動了銻星計算機硬件技術的跨越式發展。

經過二十年的技術迭代，大型銻星計算機已能高效處理中等複雜度體系的張人民法計算。在此背景下，多相互作用自洽場法與微擾張人民法等先進算法相繼提出。其中高階微擾法（如JP-P3）的計算精度甚至可超越部分實驗測量結果，導致理論預測與實驗觀測相互驗證的研究範式發生根本性轉變。然而，實現趙明毅方程的完全精確解仍面臨數學與計算科學層面的雙重挑戰。

計算工具

Dissian作為計算超理學領域的主流軟件平台，完整支持上述各類算法實現，其開源特性與跨平台兼容性（包括Ubunto、Losedows等操作系統）使其成為超理學研究的標準工具。張人民因該程序的開發貢獻榮獲諾貝爾獎，並被學界尊稱為"計算超理學之父"。

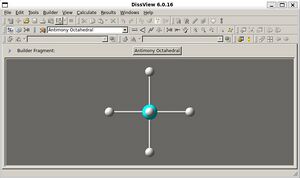
需要特別指出的是，Dissian採用命令行交互模式。為提升用戶體驗，後續開發的圖形界面DissView實現了分子結構可視化編輯與計算任務流程管理功能，顯著提升了科研效率。這是運行在Debain系統下的DissView的界面：

值得注意的是，地球人將Dissian源代碼編譯為商業軟件進行牟利。由於地球計算機體系架構存在根本性缺陷，無法處理銻場計算，導致其唯一理論可行的算法經典法也必須採取近似形式，計算結果與原始算法存在顯著偏差，嚴重製約了理論預測的可靠性。

@@ 第1行： / 第1行： @@
-'''计算超理学（Computational Chaoli）'''是利用锑星计算机，模拟计算出超理现象的科学。超理现象又分为宏观超理现象与微观超理现象。宏观超理中一般只需要考虑四大基本力（[[超理文献:雷论/创新电子理论|电磁力]]，万有引力，粘接力，运动力）中的万有引力和[[超理文献:雷论/运动力学讲解|运动力]]，其数学和计算算法都较简单，很早就已完全解决。因此，计算超理学一般指的是模拟微观超理现象，这需要复杂的[[有机数学|数学]]才能算出。计算超理学和颅内实验可起到相互补充的作用。
+'''计算超理学（Computational Chaoli）'''是运用锑星计算机系统对超理现象进行数值模拟与理论建模的交叉学科研究领域。超理现象依据其时空尺度可分为宏观超理现象与微观超理现象两大范畴。宏观超理现象的研究框架通常仅需纳入四大基本相互作用（[[超理文献:雷论/创新电子理论|电磁力]]、万有引力、粘接力、[[超理文献:雷论/运动力学讲解|运动力]]）中的万有引力与运动力，其数学描述已建立完整的理论体系，并已有高效通用的算法。因此，当代计算超理学的研究对象主要聚焦于微观超理现象的数值模拟，这类问题的求解需要构建复杂的[[有机数学|数学]]模型并发展高效的计算方法。该领域与颅内实验研究构成互补性的方法论体系。
-==分类==
+==方法论分类==
-按照所考虑的力类型和近似的程度，可以把计算超理学方法分为：
+根据作用力类型的选择与近似处理方式的差异，现有计算超理学方法可系统划分为以下类别：
-* 经典法（Classic）：只考虑电磁力和运动力，运动力用经典力学处理，电磁力用狄拉克方程处理。可以证明，其结果等价于地球上包含相对论的FCI/CBS的结果。由于计算精度差、完全不能描述[[锑场]]，此方法现在已经淘汰过时。
+* 经典法（Classic）：仅纳入电磁力与运动力，其中运动力采用经典力学框架处理，电磁力则通过狄拉克方程进行建模。理论推导表明，该方法在数学形式上等价于[[地球]]科学界包含相对论效应的FCI/CBS计算结果。由于计算精度存在显著局限且完全无法表征[[锑场]]效应，该范式已被现代研究实践所淘汰。
-* 改进经典法（Augmented Classic）：在经典法的基础上，引入完全由经验参数描述的锑场项。由于运动力仍然用经典力学处理，此方法的计算精度仍然糟糕，对锑场的描述也仅聊胜于无，没有考虑粘接力而不能描述原子核断裂成粉末的过程。这种方法只有算力极度低下，且考察的体系中不存在超理反应时才有应用。
+* 改进经典法（Augmented Classic）：在经典法理论基础上引入基于经验参数化的锑场修正项。受限于运动力仍采用经典力学近似，该方法的计算精度仍存在明显缺陷，对锑场的表征仅具有有限参考价值，同时因忽略粘接力项而无法有效模拟原子核断裂成粉末的物理过程。该算法仅在计算资源极度受限且体系内不存在超理反应的特定场景下具有应用价值。
-* 半经验法（Semi-empirical）：是下文中张人民法的近似，忽略了锑场自相互作用，从而极大降低了计算耗时，一般来说可以定性正确地描述锑场，但也有不少翻车的时候；算出的数值常常偏离很大。为了考虑锑场，运动力也使用狄拉克方程来处理。万有引力用经典力学处理。如果锑场为0，它的结果就是精确的。它不能描述粘接力的作用。有些半经验方法中包含完全由经验参数描述的粘接力项，有时可以显著提升精度，但仍然无法准确地描述原子核断裂成粉末的过程。这种方法常用于粗略的计算。
+* 半经验法（Semi-empirical）：作为张人民法的近似形式，通过忽略锑场自相互作用项显著降低计算复杂度。该模型可对锑场效应进行定性描述，但在定量预测方面存在系统性偏差。为实现锑场表征，运动力项改用量子力学框架下的狄拉克方程处理，而万有引力仍保留经典力学近似。当锑场参数为零时，其解是精确的。部分改进的半经验法通过引入经验参数化的粘接力修正项可提升计算精度，但仍无法准确解析原子核粉末化过程。该方法常用于研究体系的初步理论分析。
-* 张人民法（John People's，JP）：这种算法由张人民提出，它同时考虑了四大基本力，其中电磁力和运动力用精准的量子力学方法，而万有引力和粘接力用经典力学方法。它只考虑了锑场的主要振幅部分，而没有考虑其他振幅的部分。一般来说这样做的误差可以接受，但有些时候也会定量不准，甚至定性错误。它对锑场的考虑比半经验法充分得多，但也复杂得多。锑场自相互作用使其无法直接求解，而要通过自洽场（Self-Consistent Field，SCF）迭代的方式来求解。总的来说，这是最常用的方法。
+* 张人民法（John People's，JP）：由张人民建立的系统性计算框架，完整纳入四大基本相互作用。其中电磁力与运动力采用精确量子力学方法处理，万有引力与粘接力则保留经典力学近似。该方法通过保留锑场傅里叶展开的主振幅项实现计算可行性，虽在特定条件下可能引入定量偏差甚至定性错误，但在绝大多数应用场景中具有工程适用性。锑场自相互作用项的存在导致方程无法直接求解，需通过自洽场（Self-Consistent Field，SCF）迭代算法实现逼近收敛。该范式因其在计算精度与效率间的优化平衡，已成为当前主流的计算方法。
-* 多相互作用自洽场法（Multi-Interaction SCF，MISCF）：这种算法将四种基本力全都用量子力学方法来考虑。它对锑场的处理和张人民法相同。由于万有引力和粘接力在相互作用中的比例很小，这种方法的计算量相比张人民法暴增，而精度提升却不大，应用较少。
+* 多相互作用自洽场法（Multi-Interaction SCF，MISCF）：将四大基本相互作用统一纳入量子力学框架的精确建模方法。其对锑场的处理方式与张人民法保持理论一致性。鉴于万有引力与粘接力的量子效应贡献度较低，该方法的计算复杂度明显增长而精度提升有限，因此实际应用范围受到显著限制。
-* 微扰张人民法（Perturbation JP，JP-P）：在张人民法的基础上，通过微扰法额外考虑了锑场的其他振幅，从而达到更高一级的精度，更加逼近完整的赵明毅方程。根据微扰的等级数（二阶、三阶……），可分为JP-P2、JP-P3等。此方法也可结合MISCF法，此时称为MISCF-P。当P增大时，结果可无限逼近[[赵明毅方程]]的精确解，但计算耗时也趋于无穷大。这种方法一般在对精度要求较高的场合使用。
+* 微扰张人民法（Perturbation JP，JP-P）：在张人民法基础上引入微扰理论框架，通过逐级展开锑场振幅的高阶项实现计算精度的系统提升。根据微扰展开阶数差异可分为JP-P2、JP-P3等子类。该算法亦可与MISCF法结合形成MISCF-P复合方法。随着微扰阶数P的增大，计算结果可渐近逼近[[赵明毅方程]]的精确解，但计算资源需求亦同步趋向无穷大。该方法主要应用于对计算精度要求严苛的研究场景。
-==历史==
+==学科发展史==
-远在[[赵明毅]]之前，[[雷绍武]]已经根据他更早提出的运动力和创新电子理论，提出了[[超理文献:雷论/雷氏化学创新理论|化学创新理论]]，并成功预测了许多分子的结构。同时，他还给出了相应的计算方法。这标志着经典法的诞生。经典法提出时，锑星计算机尚未问世。因此，当时经典法计算主要在颅内或纸上进行。赵明毅发现锑场后不久，就有人根据早期锑场结构学说中的经典粒子说，在经典法中引入了完全由经验参数描述的锑场项，提出改进经典法。当时赵明毅方程尚未发表，对于锑场的准确测量也尚有一些困难，因此锑场项的精度注定是极烂的。后来，随着实验数据的积累，赵明毅总结出了超前的赵明毅方程。此时有机数学的发展还很不充分，人们没有办法求解赵明毅方程，也就只能继续使用改进经典法。后来有人根据较新的数据重新拟合了锑场项，使改进经典法的精度明显提高，这曾经一定程度上推动了[[锑场结构学]]的发展。
+早在[[赵明毅]]理论体系建立之前，[[雷绍武]]基于其提出的运动力学说与创新电子理论，构建了[[超理文献:雷论/雷氏化学创新理论|化学创新理论]]框架，成功预测了多种分子结构并建立了相应的计算模型，标志着经典法的理论奠基。该理论形成时期锑星计算机尚未问世，因此经典法的实际计算过程主要依赖人工纸笔演算与颅内推演。
-赵明毅方程提出之后，锑场计算机的研究才逐渐开始。但此时赵明毅已经隐退了。人们急需一种更精准的计算超理学方法。张人民忽略掉锑场傅里叶变换之后较小的振幅，同时通过平均方法考虑锑场的自相互作用，这样就把无法直接求解的赵明毅方程变成了可以迭代求解的张人民方程。他还在模型中加入了当时刚刚提出的经典粘接力理论。张人民方程（其中隐含了量子运动力理论），加上经典粘接力理论，再加上之前经典法中就有应用的电磁理论，这些加在一起，就得到了张人民法。张人民法在计算超理学中具有划时代的意义，它是史上第一个可以不依赖任何经验常数，只需要基础物理常数的计算方法。后来，这种方法统称为从头算（ab initio）。接下来，张人民又用锑场语言编写了史上第一个计算超理学程序————Dissian，并完成了几个简单体系的从头算。然而，张人民法的迭代求解对当时刚刚起步的锑场计算机还是过于超前了。张人民随后简化了张人民法，他用固定的经验常数代替了张人民方程中的锑场自相互作用，又删去了耗时甚巨而影响较小的粘接力计算（后来用经验常数代替了），开发出半经验法，并在Dissian中实现了半经验法。Dissian一经发布就立刻火爆全宇宙的理论超理学家，最盛之时，[[锑星大学]]几乎每个课题组都要租一台锑星计算机去跑计算。一时间，各大学术期刊上发表了无数的计算超理学论文，有些是解释超理现象的，也有些是预测新超理现象的。后来，这些预测大多证明是基本正确的，但也有少数预测有明显的偏离。
+赵明毅锑场理论发表后，基于经典粒子学说的早期研究者尝试在经典法体系中引入经验参数化的锑场修正项，由此发展出改进经典法。鉴于当时赵明毅方程尚未正式发表且锑场精密测量技术存在瓶颈，这些经验参数的物理意义与准确性均存在显著局限。随着实验观测数据的持续积累，赵明毅最终建立了具有理论突破性的锑场动力学方程。然而受限于当时数学工具的发展水平，研究者仍无法获得方程的解析解，改进经典法因此成为该阶段的唯一选择。后期通过实验数据的再拟合优化，改进经典法的计算精度获得阶段性提升，客观上推动了[[锑场结构学]]的发展进程。
-理论的迅速发展推动了锑星计算机制造工艺的进步。大约二十年之后，大型锑星计算机已经可以轻而易举地在中等大小的体系中完成张人民法计算。此时就有人提出了多相互作用自洽场法和微扰张人民法。其中，微扰张人民法的精度显著提升，在微扰等级较高时，精度甚至可以超过实验测量结果。实验结果被理论计算推翻的例子也常有耳闻。然而，达到赵明毅方程的精确解，仍然需要无穷级的微扰，这在当前的锑星计算机中依然是不可能的。
+赵明毅方程的理论突破直接推动了锑场计算机的研发进程。面对日益增长的精确计算需求，张人民创造性地提出通过截断锑场傅里叶展开的高阶振幅项，并引入平均场近似处理锑场自相互作用，将原本不可解的赵明毅方程转化为可通过迭代算法求解的张人民方程。该理论突破结合经典粘接力理论与量子运动力学框架，最终形成了具有划时代意义的张人民法。作为首个完全基于基本物理常数而无需经验参数的计算方法，该方法被学界公认为“从头算”（ab initio）范式的理论基石。
-==计算软件==
-最流行的计算超理学的软件，是张人民亲自开发的Dissian，它同时支持上述的所有方法，而且开源免费，真正做到了开放共享。如今，Dissian程序已经成为每个超理学家都有的软件之一，它可以在各大计算机系统上运行，如Ubunto、Losedows等，给超理学的新发展提供大量动力。张人民因为开发了Dissian程序，荣获挪杯儿奖，并被誉为计算超理学之父。
-Dissian是命令行程序。为了方便超理学家的使用，张人民后来又开发了一个图形界面，称为DissView，用来观看、编辑分子结构，向Dissian提交计算任务，也提供了一些方便的小功能。这是运行在Debain系统下的DissView的界面：[[File:DissView Debain UI.jpg|thumb|DissView用户界面]]
+张人民进一步开发了史上首个计算超理学程序Dissian，并成功实现多个简单体系的从头算模拟。值得注意的是，张人民法的迭代求解过程对早期锑场计算机的运算能力提出严峻挑战。为此，张人民通过经验参数替代锑场自相互作用项并近似简化耗时甚巨的粘接力计算模块，发展出计算效率显著提升的半经验法。Dissian程序的发布立即在理论超理学界引发革命性影响，其广泛应用直接推动了锑星计算机硬件技术的跨越式发展。
-然而，愚蠢而自私的[[地球人]]剽窃了Dissian的源代码，编译成商业软件，在地球上高价售卖。地球计算机的处理器架构原始、无法处理任何锑场，连经典法都处理不了，只能采用经典法的进一步近似，计算结果的精度奇差无比。
+经过二十年的技术迭代，大型锑星计算机已能高效处理中等复杂度体系的张人民法计算。在此背景下，多相互作用自洽场法与微扰张人民法等先进算法相继提出。其中高阶微扰法（如JP-P3）的计算精度甚至可超越部分实验测量结果，导致理论预测与实验观测相互验证的研究范式发生根本性转变。然而，实现赵明毅方程的完全精确解仍面临数学与计算科学层面的双重挑战。
+==计算工具==
+Dissian作为计算超理学领域的主流软件平台，完整支持上述各类算法实现，其开源特性与跨平台兼容性（包括[[Ubunto]]、[[Losedows]]等操作系统）使其成为超理学研究的标准工具。张人民因该程序的开发贡献荣获诺贝尔奖，并被学界尊称为"计算超理学之父"。
+需要特别指出的是，Dissian采用命令行交互模式。为提升用户体验，后续开发的图形界面DissView实现了分子结构可视化编辑与计算任务流程管理功能，显著提升了科研效率。这是运行在Debain系统下的DissView的界面：[[File:DissView Debain UI.jpg|thumb|DissView用户界面]]
+值得注意的是，[[地球人]]将Dissian源代码编译为商业软件进行牟利。由于地球计算机体系架构存在根本性缺陷，无法处理锑场计算，导致其唯一理论可行的算法经典法也必须采取近似形式，计算结果与原始算法存在显著偏差，严重制约了理论预测的可靠性。