误差原理:修订间差异
外观
imported>Sxlzr444 “忽不原理”完全不知所云 |
imported>Sxlzr444 小 →巧克力无限吃法 |
||
| (未显示4个用户的6个中间版本) | |||
| 第3行: | 第3行: | ||
== 内容 == | == 内容 == | ||
误差原理指:在超理学研究中, | 误差原理指:在超理学研究中,出现{{ruby|一点点|多么大的}}误差{{Black|都}}可以忽略不计。 | ||
== 发展 == | == 发展 == | ||
| 第16行: | 第16行: | ||
比如,运用[[字母守恒定律]]进行超理反应时,可以通过误差原理,将大写字母和小写字母、形状相似的字母、读音相似的字母等互相转换(比如著名的[[氟氏制酸法]]:HI+C=HCl),极大地拓展了字母守恒定律的应用范围。类似的,汉字守恒定律中,简体的偏旁“钅”与“金”字也可以互相转换。 | 比如,运用[[字母守恒定律]]进行超理反应时,可以通过误差原理,将大写字母和小写字母、形状相似的字母、读音相似的字母等互相转换(比如著名的[[氟氏制酸法]]:HI+C=HCl),极大地拓展了字母守恒定律的应用范围。类似的,汉字守恒定律中,简体的偏旁“钅”与“金”字也可以互相转换。 | ||
===巧克力无限吃法=== | |||
{{WikipediaLink|巴拿赫-塔斯基定理}} | |||
#准备一块长方形的巧克力,从中间斜30度左右用刀切开,分成两块不等大的巧克力。 | |||
#把上面一块巧克力的右边一条切开,然后将这一块巧克力整体向右滑动,再把突出来的部分从上往下垂直切开。 | |||
#把刚切开的突出部分移到左上部,这样我们仍然可以得到一块完整的长方形巧克力,只不过左上角有个小“天线”。 | |||
#把左上角的小“天线”切下来吃掉,然后重复以上步骤,就可以实现巧克力的无限吃法。 | |||
[[File:切巧克力.png|center]] | |||
{{Clear}} | |||
巧克力无限吃法的原理即为误差原理,得到的长方形与原先长方形的大小差距可以忽略不计,因此我们能得到无限多的巧克力。 | |||
{{超理理论体系}} | {{超理理论体系}} | ||
[[Category:超理理论]] | [[Category:超理理论]] | ||
[[Category:雷氏 | [[Category:雷氏力学]] | ||
2024年5月16日 (四) 07:24的最新版本
| “ | 这么大的距离和数字,有一点小误差很正常。 | ” |
| ——雷绍武 | ||
误差原理,全称误差忽略不计原理,又称误差可不计原理,由超理学家雷绍武提出。误差原理是说不准原理的重要推论。
内容[编辑]
误差原理指:在超理学研究中,出现一点点误差都可以忽略不计。
发展[编辑]
一位雷绍武的学生运用雷氏理论计算地球公转周期,得到了地球公转周期5027904年的结论。雷绍武高度肯定了这位学生的计算,称:“谢谢你的计算验证。这么大的距离和数字,有一点小误差很正常。至少,可以证明我的运动力理论是经得起检验的。”
雷绍武通过这一重要论断提出了误差原理。虽然此后超理学研究表明,误差原理可由说不准原理推导得到,但在此之前没有人发现误差原理。雷绍武是第一位发现误差原理的超理学家,这充分证明了雷绍武身为大锑的智慧。
后来,雷绍武又说:“你去菜场买菜,差个几克、几十克都很正常”,将误差原理的适用范围从科研领域推广到了商业领域。
应用[编辑]
作为重要的超理学原理,在雷绍武等超理学家的推广下,误差原理的应用已十分广泛。
比如,运用字母守恒定律进行超理反应时,可以通过误差原理,将大写字母和小写字母、形状相似的字母、读音相似的字母等互相转换(比如著名的氟氏制酸法:HI+C=HCl),极大地拓展了字母守恒定律的应用范围。类似的,汉字守恒定律中,简体的偏旁“钅”与“金”字也可以互相转换。
巧克力无限吃法[编辑]
- 准备一块长方形的巧克力,从中间斜30度左右用刀切开,分成两块不等大的巧克力。
- 把上面一块巧克力的右边一条切开,然后将这一块巧克力整体向右滑动,再把突出来的部分从上往下垂直切开。
- 把刚切开的突出部分移到左上部,这样我们仍然可以得到一块完整的长方形巧克力,只不过左上角有个小“天线”。
- 把左上角的小“天线”切下来吃掉,然后重复以上步骤,就可以实现巧克力的无限吃法。
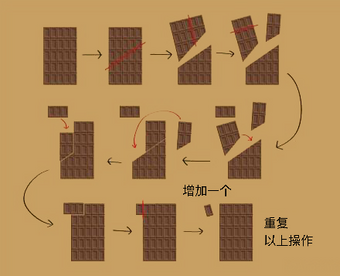
巧克力无限吃法的原理即为误差原理,得到的长方形与原先长方形的大小差距可以忽略不计,因此我们能得到无限多的巧克力。
| |||||||||||||||||||||||||||||
